Seminars

43rd KPP Combinatorics Workshop - Dec 18 2010

secttitle:	Dec 18 (Saturday), 2010
Time:	11am - 5:30pm ( Dinner from 6pm )
Location:	College of Natural Sciences, Building 1, Room 213

Schedule
11:00 - 11:50	Dan Drake KAIST, Daejeon	Paths, polynomials, partitions, and paths
12:00	Lunch
1:30 -2:20	Byungchan Kim Seoul National University, Seoul	Combinatorics of Partial Theta Functions
2:30 -3:20	David Cariolaro Xi’an Jiaotong-Liverpool University, China	Excessive Factorizations
3:40 - 4:30	Jung Wook Lim Postech University, Pohang	Zero-divisor graphs over a commutative ring
4:40 - 5:30	Shinya Fujita Gunma National College of Technology, Japan	Rainbow Ramsey Numbers and Related Topics
6:00	Dinner

Abstracts

Dan Drake
Paths, polynomials, partitions, and paths

We start with weighted Motzkin paths, then discuss how those paths are the basis of a combinatorial theory of orthogonal polynomials. Four sets of "classical" orthogonal polynomials naturally describe a hierarchy of noncrossing complete matchings, complete matchings, set partitions, and permutations. From matchings and set partitions, we move on to consider$k-distant noncrossing matchings and set partitions, and end with a bijection from 2-distant noncrossing matchings to weighted Motzkin paths, thus returning us to where we started.

Byungchan Kim
Combinatorics of Partial Theta Functions

A partial theta function is a sum of the form 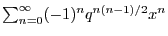$\sum_{n=0}^{\infty} (-1)^{n}q^{n(n-1)/2}x^{n}$ . Combinatorially, identities containing partial theta function are very interesting since they indicate what remains after numerous cancellations of certain kinds of partitions. In this talk, we will discuss the combinatorics of some identities involving partial theta functions in Ramanujan's lost notebook.

David Cariolaro
Excessive Factorizations

An excessive factorization of a graph

is a minimum set of perfect matchings of

whose union is

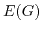. The excessive index of

is the number of perfect matchings in an excessive factorization of

(or $\infty,$ if the graph does not admit an excessive factorization). More generally, let

be a positive integer. An excessive -factorization of a graph

is a minimum set of matchings, all of size exactly

, whose union is the edge set of

. The excessive -index of

is the number of matchings in an excessive

-factorization of

(or $\infty,$ if the graph does not admit an excessive

-factorization).

In this talk we shall aim to give an introduction to the theory of excessive (and excessive -)factorizations.

The content of this talk is joint work with Arrigo Bonisoli, Hung-Lin Fu, Giuseppe Mazzuoccolo and Romeo Rizzi.

Jung Wook Lim
Zero-divisor graphs over a commutative ring

In 1988 , Beck first introduced the concept of zero-divisor graphs over a commutative ring with identity. Especially, he was interested in coloring problems. Later, in 1999, Anderson and Livingston defined a new concept of zero-divisor graphs over commutative rings. Following Anderson et al., the zero-divisor graph of a commutative ring

, denoted by $\Gamma(R)$ , is the graph with vertices

, the set of nonzero zero-divisors of

, and for distinct $x, y \in Z(R)^*$ , the vertices

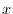and

are adjacent if and only if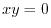

. In the first part of this talk, I will survey some properties of zero-divisor graphs. Next, I will prove some basic results about the zero-divisor graphs of the rings

and $A+XB[\![X]\!]$ , where $A \subseteq B$ is an extension of commutative rings with the same total quotient ring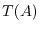

Shinya Fujita
Rainbow Ramsey Numbers and Related Topics

Gallai-colorings of complete graphs - edge colorings such that no triangle is colored with three distinct colors - occur in various contexts such as the theory of partially ordered sets (in Gallai's original paper), information theory and the theory of perfect graphs. A basic property of Gallai-colorings with at least three colors is that at least one of the color classes must span a disconnected graph. We are interested here in whether this or a similar property remains true if we consider colorings that do not contain a rainbow copy of a fixed graph F. In this talk, I will introduce some recent results on this topic, and I will also mention a related topic concerning rainbow ramsey numbers.