37th KPP Combinatorics Workshop - January 16 2010
Date: January 16, 2010
Time: 11am - 5:30pm ( dinner from 6pm )
Location: School of Natural Sciences Room 218

Schedule
11:00 Jeong Ok Choi
Trinity College, Connecticut, USA 		A decomposition problem of regular hypergraphs
12:00 Lunch
1:30 Hye Jin Yoon
Kyungpook National University, Daegu 		On the Bollobas-Riordan polynomial of covering ribbon graphs
2:30 Seog Jin Kim
Konkuk University, Seoul 		Identifying Codes in q-ary Hypercubes
3:30 Jack Koolen
Postech University, Pohang 		Hoffman graphs with smallest eigenvalue -3
4:30 Suyoung Choi
Osaka City University, Osaka, Japan 		Cohomological rigidity of reducible simplicial polytopes
6:00 Dinner

Abstracts

Jeong Ok Choi
A decomposition problem of regular hypergraphs

An $ r$-block is a $ 0,1$-matrix in which every row has sum $ r$. Let $ S_n$ be the set of pairs $ (k,l)$ such that the columns of any $ (k+l)$-block with $ n$ rows split into a $ k$-block and an $ l$-block. We determine $ S_n$ for $ n\le 5$. In particular,
$ S_3=\{(k,l) \colon 2\mid kl\}$,
$ S_4=\{(k,l) \colon (6\mid k\textrm{ or } l)\textrm{ and } (1\notin\{k,l\})\}$, and
$ S_5=\{(k,l) \colon 11\ne\min\{k,l\}>7$ and each value in $ \{3,4,5\}$ divides $ k$ or $ l\}$.
The problem arose from a list-coloring problem in digraphs and is a refinement of the notion of indecomposable hypergraphs. This is joint work with Douglas B. West.

Hye Jin Yoon
On the Bollobas-Riordan polynomial of covering ribbon graphs
It is well-known that the Jones polynomial of a knot is related to the Tutte polynomial of a spacial graph obtained from a regular projection of the knot. The Bollobas-Riordan polynomial is the generalized version of the Tutte polynomial which is related to the Kauffman bracket polynomial of the corresponding ribbon graph. In this paper, we review the construction of the covering ribbon graphs from a voltage assignment and study the Bollobas-Riordan polynomial of the covering ribbon graphs in terms of the Bollobas-Riordan polynomial of the base ribbon graph and the voltage assignment. And we calculate some Bollobas-Riordan polynomials of the covering ribbon graph about simple ribbon graphs.
Seog Jin Kim
Identifying Codes in q-ary Hypercubes
Let $ q$ be any integer $ \ge 2$. In this paper, we consider the $ q$-ary $ n$-dimensional cube whose vertex set is $ \mathbb{Z}_q^n$ and two vertices $ (x_1, \ldots, x_n)$ and $ (y_1, \ldots, y_n)$ are adjacent if their Lee distance is $ 1$. As a natural extension of identifying codes in binary Hamming spaces, we further study identifying codes in the above $ q$-ary hypercube. We let $ M_t^{q}(n)$ denote the smallest cardinality of $ t$-identifying codes of length $ n$ in $ \mathbb{Z}_q^n$. Little is known about ternary or quaternary identifying codes. It is known that $ M_1^{2}(n) \ge \frac{2v}{d+1 + \frac{2}{n}}$ where $ v$ is the number of vertices of $ \mathbb{Z}_2^n$ and $ d$ is the degree of any vertex of $ \mathbb{Z}_2^n$. In a similar manner, we show that $ M_1^{q}(n) \ge \frac{2v}{d+1 + \frac{1}{n}}$, where $ d$ is the degree and $ v=v(q)$ is the number of vertices of $ \mathbb{Z}_q^n$ for $ q=3$ and $ q=4$, respectively. This is joint work with Jon-Lark Kim.
Jack Koolen
Hoffman graphs with smallest eigenvalue -3
A line graph has smallest eigenvalue -2. In 1976 Cameron et al showed that except for a few exception all graphs with smallest eigenvalue -2 are generalized line graphs, that is, a line graph with Cocktail party graphs attached in a certain way. In 1977 Hoiffman showed that the next limit point equals -1 - 21/2 (coming from the cartesian product of a complete graph with a path of length 2.) In recent years the work of Hoffman has been extended by Woo and Neumaier(1995) and Taniguchi(2009), using the concept of Hoffman graphs. in this talk i will discuss the Hoffman graphs with smallest eigenvalue -3.
Suyoung Choi
Cohomological rigidity of reducible simplicial polytopes
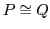A simplicial (or simple) polytope $ P$ is said to be cohomologically rigid if whenever there exists another polytope $ Q$ with an isomorphism of their Tor-algebra there is a combinatorial equivalence $ P \cong Q$. In this talk, we find a necessary condition to be combinatorially rigid for $ 3$-dimensional reducible simplicial polytopes. This question is quite related to so-called toric topology. We also discuss about the relation between theory of polytopes and toric topology.
Last Modified: 2022. 04. 05. (화) 13:40:48 KST